賠率的“陷阱”：沒有尾部對沖的投資者，就不該留在賭桌上

　　本文的標題有兩重含義：

• 　　賠率之“成為陷阱”，導致致命風險；

• 　　賠率之“作為陷阱”，贏得超額回報。

　　一

　　假如你是一個原始人。

　　你即將迎來人生的一次艱難抉擇。

　　有一天，你打算出門為自己的家人和孩子採摘一些野果。

　　你知道，你家洞穴不遠處，有一片漿果林。

　　那裡的野果鮮美多汁，維生素含量豐富，大人小孩都愛吃。

　　可是，那片果林附近經常有黑熊出沒。

　　人生艱難，自古沒有免費的午餐。

　　然而，望著孩子們嗷嗷待哺的眼神兒，你湧出一股無私的大無畏精神，決定去冒險。

　　儘管你的“無私”，可能只是“自私的基因”為了繁衍後代而製造出來的幻覺。

　　你小心翼翼地來到果林，左顧右盼，一邊摘果，一邊觀察，提防黑熊從陰暗角落衝出來。

　　看來今天運氣不錯，你很快裝滿了大半籃子漿果。

　　該見好就收了，你抱緊籃子，一半歡喜一半緊張地走上了回家之路。

　　這時，你遭遇了比地球還要久遠的“墨菲定律”：

　　你最擔心的事情，在你不情願的時刻，終於發生了。

　　你發現右側的叢林裡有一個黑影！

　　熊來了？

　　百萬年的演化進程，贈予你天生擁有的直覺，這類直覺讓你能夠迅速洞察危險，並且逃命。

　　這類直覺，是靠沒能及時逃命的原始人被吃掉而選擇並遺傳下來的。

　　然而，儘管你對熊有很好的直覺，那個黑影也可能是塊石頭。

　　一個艱難的抉擇擺在你面前：

　　選擇1：該猜那個黑影是只打算吃掉你的黑熊，然後為了逃命而扔掉辛苦採摘的鮮果嗎？

　　可是你腦海裡彷彿看到孩子們失望的眼神，以及未來幾天餓肚子的煎熬。

　　選擇2：該賭一下那個黑影只是個石頭，然後你抱緊籃子快速（比空手跑慢一半兒）離開嗎？

　　二

　　那個黑影到底是熊，還是石頭？

　　讓我們計算一下。

　　先做兩個假設。

　　假設一：對熊或石頭的判斷準確率。

　　原始人對熊的直覺判斷不低，但考慮到緊張情緒，所以我們估計原始人判斷是黑熊還是石頭的準確率高達60%。

　　假設二：森林裡像熊的石頭與熊的比例。

　　一隻熊的平均居住面積大約有幾十平方公里，而石頭的數量則要多得多，我們姑且認為石頭和熊的比例是10:1。

　　這時，原始人看見一個黑影，並且直覺告訴他可能是隻熊，請問：

　　真的是一隻熊的概率是多大？

　　請允許我畫一下：

　　第一步，看一下樹林裡（像熊的）石頭與熊的總量，數量上是10比1，如下圖⬇️。

　　第二步，假如那個黑影是石頭，因為原始人的準確率為60%，所以60%的時候他準確地猜出是石頭，40%的時候誤以為是熊，如下圖⬇️。

　　第三步，同理，假如那個黑影是熊，因為原始人的準確率為60%，所以真的是熊並且原始人也猜對的概率是60%，如下圖的右上角⬇️。

　　第四步，因為原始人觀察到是熊，讓我們去除掉“他不認為是熊”的可能性，如下圖⬇️。

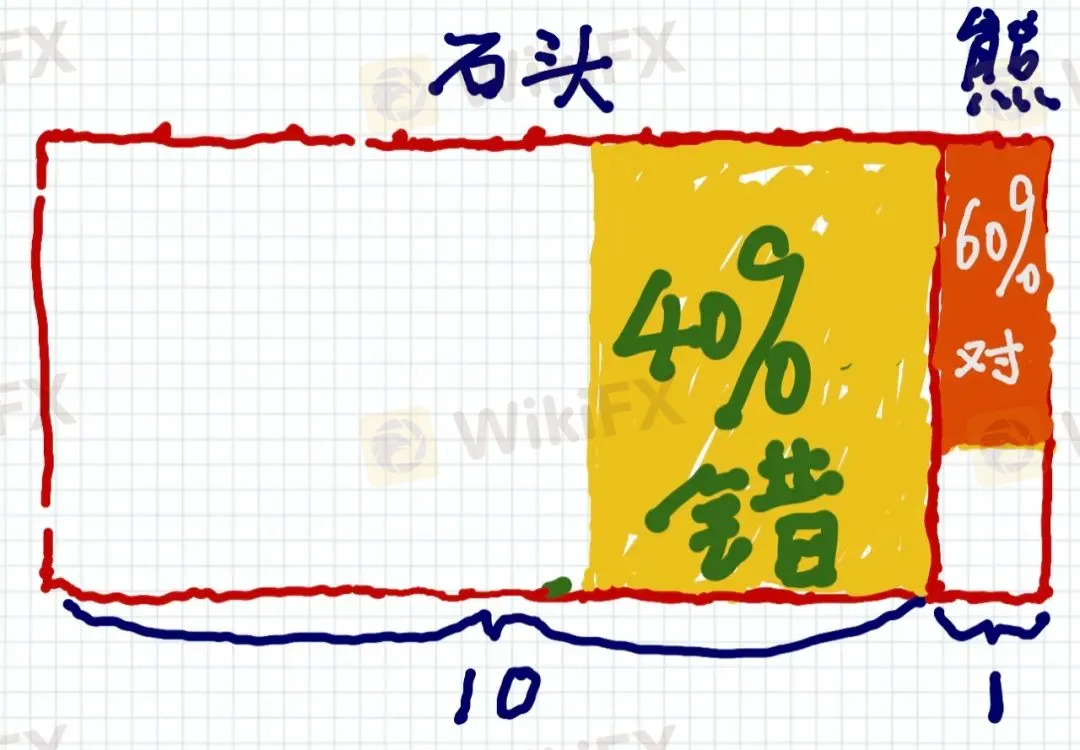
　　第五步，我們算一下，原始人觀察到的熊，由如下兩類可能構成，計算如下圖⬇️。

　　第六步，在上圖觀察中，只有右側橙色的部分，真的是熊，所以我們要計算：當原始人觀察到是熊，其實真正是熊的可能性有多大，如下圖⬇️。

　　也就是說，你以為是熊但實際上真的是熊的可能性，只有13%。

　　倒過來說，就是其實你有近90%的可能性是安全的。

　　多大的概率呀。

　　要是有個你熟知的大老闆給你一個準確率高達“90%”的內部消息，讓你去買他們公司“肯定會大漲”的股票，你會不會買？

　　你是不是覺得：人生能有幾回搏？而且索羅斯和老喻都說過，大機會來臨時要下大注，於是你推上一大堆籌碼。有些人甚至會藉錢抵房。

　　然而，原始人畢竟是原始人，他扔下了辛苦採摘的一籃子漿果，掉頭就跑了。

　　聰明人可能坐不住了，著急要說：

• 　　這不就是一個簡單的貝葉斯計算嗎？

• 　　這不就是卡尼曼說的“系統一”和“系統二”嗎？

　　慢，到目前為止，還只是鋪墊，高潮還在後面。

　　的確，這是一個貝葉斯計算。假如有個愛思考的孩子能看到這個過程，亂畫一番的我就很心滿意足了。

　　95%看過《思考快與慢》的，都記住且僅記住了“系統一”、“系統二”：

• 　　系統一是直覺、條件發射、不動腦筋、經驗主義，與杏仁核有關；

• 　　系統二是三思而後行、深思熟慮、主動思考，與前額葉皮層有關。

　　那麼，原始人的“系統一”，到底是理性，還是非理性？

　　考慮到原始人怕被吃掉，現在社會已經沒有熊從背後拍你肩膀咬你脖子的可能性了，但百萬年很長，數千年文明很短，所以人類基因還在支配著我們的“系統一”。

　　所以，對於現代人而言，“系統一”大多是非理性的。你贊成嗎？

　　然而，有個人不贊成。

　　三

　　這個人，就是喜歡罵各種牛人的自戀狂塔勒布。

　　在《非對稱風險》裡，他點名罵了理查德·塞勒：

　　（他們）試圖把我們的行為區分為“理性”與“非理性”（非理性就是偏離了預想值或預先設定的模型的行為），然而他們全面誤解了概率論的適用性，又過分依賴於一階模型。

　　他們還傾向於將復雜事物理解為若干變量的線性組合，他們認為我們只要理解了微觀個體，就能掌握大眾和市場的規律，或者只要我們理解了螞蟻，就能理解龐大的蟻穴的構造。

　　塔勒布罵人不奇怪，但罵塞勒還是讓我有點兒意外。

　　塞勒算是特立獨行的人，開創了行為金融學，得了諾獎，有自己的資產管理公司，還演了《大空頭》（請注意，這部電影是對“反向黑天鵝”的精彩演繹），並且他對“熱手謬誤”的解釋，也說明他是一位“概率思考者”。

　　按理說，塞勒是“塔勒布最喜歡罵的那些人”也喜歡罵的人，卻沒有因此實現“敵人的敵人就是朋友”。

　　塔勒布罵塞勒的理由是：

　　他們混淆科學與唯科學主義的區別，他們甚至認為唯科學主義比科學更具科學性。

　　罵完了不說，塔勒布還給“塞勒們”創造了一個詞：

　　“白知”（intellectual yet idiot），它特指那些高智商的聰明的白痴。

　　我們來學一下知識分子如何罵人：

　　“白知”總是將那些自己無法理解的行為定義為反常、特例、病態和非理性，卻沒有意識到可能是自己的理解力有限。

　　他們認為人們的行為應該遵循利益最大化原則，而他們能夠知道別人最大的利益是什麼，尤其是那些鄉下的農民和發不出清脆元音並支持英國脫歐的底層人士。

　　當平民按照自己認為合理而“白知”卻不能理解的方式做事情的時候，“白知”就會說他們“沒有教養”。

　　太有趣了。

　　其實卡尼曼和塞勒是一脈相承的，但塔勒布並沒有罵卡尼曼，可能因為卡尼曼誇過塔勒布的書吧。

　　而且，塞勒對於投資的三觀，和塔勒布非常接近，儘管路線不一樣。

　　塞勒創立的資產管理公司，專門尋找投資者對公司發展反應過度或不足時產生的划算買賣，其原理是基於“投資者總是過度自信或過度恐懼”，據說業績不錯。

　　塞勒給投資人的建議是：

　　最好的策略是創建一個明智的長期投資組合，然後忘記它。

　　讓我們還是把話題扯回你：

　　一個正在面臨艱難抉擇的原始人。

　　四

　　在本文開篇的案例裡，我們計算了“看成熊的情況下真的是熊的概率”，這個數值是13%。

　　但是，這個計算忽略了一個重要的環節：

　　賠率。

　　由於被熊吃的極端事件，很難在現代社會出現，讓我們假設你被熊咬了一下，逃生了，回到村里，神醫給你治好了，要價100籃子漿果。

　　接下來，我們再簡單計算一下（忽略籃子的價值）：

　　情況1： “看成熊的情況下真的是熊的概率”，是13%；

　　情況2： “看成熊的情況下但不是熊的概率”，是87%。

　　大概率不是熊，為什麼要跑呢？

　　我們在前面概率計算的基礎上，在引入“賠率”來算一下。

　　假如選擇不跑：

　　情況1： 13%的可能性發生，損失是100籃水果；

　　情況2： 87%的可能性發生，收益是1籃水果。

　　計算收益如下：

　　13%✖️（-100）➕87%✖️1=（-12.13）

　　也就是說：

　　選擇不跑，從概率上是佔優的，但從賠率上是吃大虧的。

　　所以，作為原始人的你，應該立即扔掉籃子，撒腿就跑。

　　由此，我們也能理解，塔勒布罵塞勒的原因之一了。

　　巴布亞新幾內亞居民有種“建設性偏執”：不要在一棵死樹下睡覺。

　　這是迷信嗎？可能。但也可能是基於經驗的概率統計結果。

　　這是非理性嗎？

　　塔勒布的評論是：只要你不在一棵容易被風刮倒的死樹下睡覺，你就不容易被它砸中，其他都不重要。

　　所以，某些偏執，或者原始人的“慌亂”，也許是一種有效的風險防控手段和自我保護機制，以避免不可承受之風險的發生。

　　正所謂：不聽老人言，狗熊在眼前。

　　五

　　我如此不厭其煩地講述“熊來了”的故事，是因為看到戴國晨寫塔勒布新書《肥尾分佈的統計效應》的讀後感，其中有下面這段：

　　總的來說，概率只是積分內部的核函數，真實世界中重要的是賠付，也即概率事件對每個人的實際影響。

　　期望值的計算，只是小學二年級水平的數學難度，但是很多專業人士，在這裡都可能會犯糊塗。

　　但關鍵點還不在這裡，科學的進步，讓人類越發相信自己征服“未知”的力量，不管是對自然界，還是在金融領域。

　　但是，未來很難預測。

　　而且，即使你在概率層面預測“正確”，但是因為忽略了賠率，尤其是低估了黑天鵝事件造成的摧毀，那麼這個“神預測”也不能幫你賺錢。

　　由此，塔勒布給出了他的哲學：

　　反脆弱，不用做預測大師，只需要改變賠付關係即可。

　　為什麼呢？

　　因為：在肥尾分佈下，你很難進行“正確量級的預測”。

　　我在下一節，將從另外一個“簡單的”角度，來講述預測的艱難之處。

　　那該怎麼辦呢？

　　戴國晨的文章裡總結了策略如下：

　　金融領域風險管理的本質在於改變賠付關係，而不在於追求正確預測，因此只要在賠付關係上有利於自身，哪怕降低預測精度也無妨。

　　如前所述，《大空頭》裡，上演的正是這樣一個故事。

　　但是，這裡面的要點，卻被廣泛地誤讀。

　　人們總覺得，《大空頭》裡的贏家，靠的是“準確預測了次貸危機”。

　　事實並非如此。

　　可以想像，在電影裡的那幾批幸運傢伙之外，一定還有很多人，或早或晚預測了同樣的事情，例如有些人可能一直就在看空房地產，但為什麼偏偏是這幾批人呢？

　　是因為運氣好嗎？

　　當然，運氣永遠是排在第一的短期因素。

　　更關鍵的是，當時出現了極好的賠率，這才是關鍵。

　　哪怕當時“大空頭”的預測者錯上幾十年，根據他們買入的籌碼的賠率，他們都不會虧。

　　可是，人們更願意相信“預測”的神勇。

　　連當事人自己也會信，例如在次貸危機中大賺的保爾森，在隨後的美股大牛市中，虧得一塌糊塗。

　　一旦你的預測依賴於時間的精確，那就更麻煩了。

　　因為預測一件事情可能會發生，比預測一件事情什麼時候發生，要更靠譜一些。

　　莫言就說過：中國應該還會有人拿他那個獎，但具體啥時候不知道。

　　再比如，大多數賣空的玩家，會努力計算金融泡沫的時間，環球資本的馬克·施皮茨納格爾則不一樣。

　　馬克·施皮茨納格爾就是在2020年3月份賺了幾十倍的那個傢伙。

　　他是這麼做的：

• 　　不管局勢好壞，他始終不吝以連續小虧為代價保持充足的看跌期權。

• 　　一旦市場失控，這些期權立馬就會比成本價漲上幾千倍。

　　不依賴於時間的精確性，但享受時間的長期性所帶來的遍歷性，這才是做時間的朋友。

　　預測的準確率經常不靠譜，而確定的賠率，尤其是具有優勢的賠率，會令較小概率的預測隨著時間疊加成較大概率的優勢。

　　賠率令時間成為朋友，反之則是敵人。

　　尤其是，從永久性損失看：

　　預測準確率的提高如果對應賠付的大幅惡化，這樣的準確並沒有意義。

　　於是，就有了引發我寫此文的那句話：

　　如人們所說，同樣是犯錯誤，把熊誤認為是石頭遠遠比把石頭誤認為是熊糟糕得多！

　　六

　　這裡面，還有一個很好玩兒的地方。

　　不知道你發現沒，“熊來了”的這個故事裡，出現了三個概率數值的兩次反轉。

　　第一個概率，是“原始人識別熊還是石頭”的準確率，高達60%。

　　於是，原始人的反應是：

　　熊來了，快跑！

　　第二個概率數值是“熊和像熊的石頭”之間的比例，其中是熊的概率為1/（10+1）。

　　因為第二個概率是基礎比率，導致了第一次反轉：

　　“你以為是熊但實際上真的是熊”的可能性，只有13%。從你直覺的較大概率事件變成了較小概率事件。

　　哎，90%的可能性不是熊，別跑！

　　第三個概率數值與期望值有關，是賠率，被熊咬和跑掉之間的賠付比例是100:1。

　　結果，賠率造成了“第二次反轉”：

　　小概率發生的事情，因為對應賠付損失極大，所以我們更應該重視小概率，而忽略所謂的“大概率優勢”。

　　啊，雖然小概率是熊，被咬了賠不起，快跑！

• 　　造成第一次反轉的，是因的因；

• 　　造成第二次反轉的，是果的果。

　　這個蹺蹺板式的遊戲，真有趣。

　　多次反轉，因果交織，在現實中經常出現。

　　例如2020年的危機，你該如何預測？

• 　　因為疫情，股市大跌；

• 　　因為經濟糟糕，各國出台政策刺激；

• 　　因為錢多了，人們紛紛擠入龍頭股，管它價格多高...

　　疫情等因素引發的多次反轉型市場波動，連最厲害的文藝復興基金都被破了金剛不壞身。

　　對於罕見的虧損，西蒙斯解釋說：

　　該公司的虧損是由於在3月份的暴跌中對沖不足，然後在四月至六月的反彈中對沖過度所致。發生這種情況是因為模型對最初的問題進行了“過度補償”。

　　文藝復興基金依賴於歷史數據訓練出來的模型，當市場反轉又反轉時，模型被來回拉鋸，而且總是“晃過頭”，像是被馬拉多納的假動作晃暈了的後衛。

　　我不由得想起“三體問題”：

• 　　現在已知，三體問題不能精確求解，即無法預測所有三體問題的數學情景。

• 　　受初始狀態影響的敏感性，初始條件非常微小的變動也可以導致最終狀態的巨大差別。

　　很多時候，人類不得不預測，例如原始人必須要預測“黑影是不是熊”。

　　但是我們要理解預測的局限性，並探索如何應對。

　　格林斯潘說：經濟學家預測出了過去5次衰退中的9次。

　　然而，我們卻總是相信預測，迷信專家。

　　你去看看滿大街股票預測專家們的生意。

　　“股票預測專家惟一的價值，就是讓算命先生看起來還不錯。”

　　巴菲特如是說。

　　時間也許願意做你的朋友，但討厭被你看穿。

　　七

　　“好了，就算你說得有道理，那你說該怎麼辦呢？”

　　難道我們能做的就是和原始人一樣，熊來了就跑？

　　我們廣大散戶（包括我自己哈）不正是這樣做的嗎？

　　嗯，批評算命先生的文章，也無法逃離當算命先生的宿命。

　　為了本文閱讀票房，請允許我給出一個模糊的科學算命：

　　一個原始人，該如何應對“熊來了”？

　　塔勒布老師的藥方是：

　　在黑天鵝降臨之時，具備反脆弱特性的事物不但不會受損，反而還能有巨大收穫。

　　具體該怎麼做呢？

　　原始人扔掉漿果，逃回山洞，在家人怨恨的目光下，陷入了深深的思考。

• 　　狗熊可以吃人，人為什麼不能吃狗熊呢？

• 　　因為狗熊力氣太大，村里人一起圍攻也搞不掂。

• 　　但是，聽說隔壁村兒搞了個高科技，叫“陷阱”，能抓住熊。

• 　　可是，用陷阱抓熊的概率太低了。

• 　　慢著，假如大規模生產“陷阱”，會不會算得過來帳呢？

• 　　再進一步，我們能否在漿果樹林附近多挖陷阱，這樣一方面保護我們摘果，而且會增加狗熊掉入陷阱的概率。

• 　　時間長了，總會有狗熊掉進陷阱。這就叫遍歷性。

• 　　哪怕很久才抓住一隻狗熊，但是回報實在太豐厚了，那肉也夠吃上好幾個月，熊皮還能做馬甲呢。

　　嗯，這樣我們平時吃漿果，然後隔一陣子抓一隻大肥熊，生活充滿了希望！

　　這的確是一個看起來很美好的模型。

　　數學上也很容易解釋：儘管抓住熊的概率很低，假設每天熊掉入陷阱的概率是1%，那麼連續n天熊不掉入陷阱的概率，是99%✖️99%✖️99%......

　　這時候，你才會感受到，複利在幹壞事兒的時候才厲害！

　　99%這個大概率數字，不斷乘下去，會一點點累積成一個小概率。

　　因為熊掉入陷阱的概率是“1-99%✖️99%✖️99%......”，所以就變成了大概率事件。

　　這就是低成本陷阱的數學原理。

　　在現實中，的確也有這樣的事物。

　　八

　　管理著43億美元的環球投資，做的就是這樣的生意：

　　主動小虧，偶爾賺入超級大錢。

　　福布斯雜誌這樣介紹道：

　　環球投資購入短期期權合約。這種金融工具的用途是規避市場劇烈波動以及金融市場崩盤，兼具“深凸性”和“虛值”兩種性質。直白點說，只有市場突發大崩盤，這種交易才有得賺。

　　2020年三月，環球投資旗艦基金“黑天鵝事件預防協議”取得驚人的3,612%的回報率，令全年回報率一舉躍升至4,144%。

　　然而，我想說的是，道理似乎誰都懂，真正賺到錢很難。

　　從2009年到2019年，美股迎來一場超級大牛市，許多類似環球投資的尾部風險對沖基金都虧得一塌糊塗。

　　這類案例，在常識層面會給人以啟發，也會實實在在地指導我們在投資乃至人生上的行動。

　　但是，作為成功神話，環球投資可能會“誤導”太多人：

• 　　我每天堅持買彩票算不算以極小成本博無限大的收益呢？

• 　　我用90%的資金買指數基金和貨幣基金，用10%的資金炒期貨，算不算啞鈴策略呢？

　　當然都不是。

　　彩票和個人炒期貨，都是負期望值，單憑這一點，就令絕大多數參與者穩穩地輸光本金，並且毫無希望。

　　期望值是否為正，區分了賭徒和投資人。

　　即使期望值為正，你也要依賴於大數定律的實現。

　　但事實上，對於個人而言，你可能很難實現強大數定律的“足夠多次”。

　　布魯斯·紐伯格說過：“概率與結果之間存在巨大的差異。可能的事情沒有發生（不可能的事情卻發生了）向來如此。”

　　根據幾何分佈，你要扔14.7次骰子，才能讓6個數字每個都至少都出現一次。你要和37.2個人交往，才能做到“和所有星座的人都談過戀愛”。

　　也就是說，即使有了正期望值，你還需要遍歷性。

　　太難了。

　　同樣是利用“黑天鵝+肥尾效應”賺錢，塔勒布自己都熬不下去，據說後來的收益也一般。

　　環球投資的成員有十多位博士、數學家、交易專家。創始人馬克·施皮茨納格爾16歲就跟著一位期貨高手打暑期工，身經百戰，又去了紐約大學數學研究院師從塔勒布。

　　當年與塔勒布合作成立對沖基金Empirica，馬克·施皮茨納格爾才是不斷虧錢時不哆嗦的那個人，塔勒布反倒嚇得要命。

　　此外，環球投資看起來也很會做生意，也就是募集資金，因為基金總是需要彈藥的。

　　環球投資的產品，被形像地稱為“巨災保險”，客戶多是錢很多的金融機構，比如養老基金、主權基金（據說當年也向中國推銷過）。客戶指定部分需要上“保險”的資產，向環球投資額外提供一部分資金，環球投資管理並對額外資金收取相應的提成。舉個個人投資者熟悉的例子，我們都知道指數基金投資最適合業餘投資者，那麼，如果我們採用塔勒布的“啞鈴策略”，用大部分的指數基金，加小部分的尾部風險對沖，結果會怎麼樣？馬克·施皮茨納格爾在2020年初的致股東信中（看來敢於給股東寫信是個值得關注的投資信息）做了一個數據模擬：

• 　　持有96.7%的標普500和3.3%的環球投資的“巨災保險”，在過去十年的投資回報是319%。

• 　　不僅好於僅僅持有標普500，也好於那些配置75%標普500和25%其他資產的組合。

• 　　更何況，這個數字還沒有包括一季度的40倍！

　　你看，環球投資的策略，像不像我上面編造的那個“熊來了”的故事，一個人想出了一個模式：

　　他對那些採漿果的人們募集資金，然後挖下了一個個捕捉黑熊的陷阱。

　　只要抓住一隻大黑熊，他就能夠賺回所有的陷阱成本。

　　所以，那些採漿果的人們，就向他付錢，相當於為自己的漿果投資買下了保險。

　　於是，“熊來了”這件令原始人恐懼並且不可承受的事情，因為陷阱的出現，變得值得期待，甚至可能帶來肥美的收益。

　　環球資本作出了示範：

　　“在黑天鵝降臨之時，具備反脆弱特性的事物不但不會受損，反而還能有巨大收穫。”

　　九

　　投資最重要的事情，到底是什麼？

　　綜上所述，應該是：

• 　　別被熊吃了。

• 　　別在死樹下睡覺。

　　由此可見，投資的第一原則是：永遠不要虧（大）錢。

　　第二條原則是：永遠不要忘記第一條規則。

　　對於投資者而言，最重要的風險，是永久損失的可能性風險。

　　但是，為了躲避熊，不去摘果子，什麼都不做躲在山洞裡，也不是回事兒。

　　從“熊來了就跑”，到給熊挖陷阱，首要目的不是為了利用黑天鵝事件發大財，而是規避風險。

　　對於原始人而言，給熊挖陷阱是為了對沖風險，守護自己採摘漿果的收益。

　　假如你沒有用於對沖風險的“捕熊陷阱”，就不要出去摘果子。

　　說個我自己親身的經歷吧。

　　為了避免任何小樣本的偏差與誤導，我用的是自己“虛擬賭博”的案例。

　　最近我經常在吃飯的時間，忙裡偷閒，在野狐圍棋旁觀高手對局，順便下注。

　　基本上我只選擇AI與人類的對局，因為AI水平相當穩定，只要看準了勝率和賠率，控制好下注比例，基本上穩贏。

　　靠此策略，我穩穩地從幾千塊錢（虛擬幣）的窮光蛋，成為資產高達五百萬的棋迷。

　　昨天晚飯時，AI們似乎都在休息，我只看到了兩個人類業餘“9段”在對局，點進去看了一下，發現局面非常傾斜，黑棋優勢極為明顯，於是我沒有遵守自己的“投資框架”，下注於雙方都是人類的對局。

　　開始的時候，我還意識到自己在冒險，所以即使黑棋優勢非常明顯，“第一階段”我還是只下注了40萬，佔總資產不到10%。

　　該局一共有三個階段下注，每個階段的賠率，會因為局面的進程而調整。

　　1、第一階段下注40萬，對應的是本金之外（下同）50萬的預期收益。

　　2、到了第二階段，局面朝我預期的方向發展，黑棋的盤面優勢高達二十多目。

　　這算是大機會了，於是我加註100萬，因為局勢更明朗了，所以賠率下降，這100萬對應的是80萬的收益。

　　3、又過了一會兒，黑棋唯一的一塊孤棋也安全了，馬上進入收官階段，白棋很難翻盤了，賠率居然還沒變，我趕緊又加註了100萬。

　　這兩百萬，約占我總資產的40%。

　　4、接下來進入了第三階段。

　　這時候，白棋拼命反撲，盤面目數的差距越來越小，但是白棋的代價是出現了一塊孤棋，面臨死活問題。

　　我算了一下，這道死活題不難，黑棋可以從內部滅眼盡殺白棋。果然，觀棋區有個3段也擺出了變化，可見的確簡單。

　　我翻看了一下第三階段的賠率，這時大家都看出白棋無回天之力了，白棋獲勝的賠率是1賠6。看油水不大，我沒有再加註，哪怕幾乎是穩贏了。

　　這時候，我的投資總覽如下：

　　5、此刻，我突然冒出一個念頭：

　　現在我一共下注了240萬，賭黑棋贏，對應的是210萬收益。

　　根據第三階段的賠率，假如我反向，押注於弱勢的白棋一方，只需下注50萬，對應250萬的收益，就可以實現對沖：

　　不管黑白那一方贏，我都能賺錢。

　　如下圖：

　　這就是安全套利吧！

　　然而我並沒有這麼做。

　　難道下黑棋的9段看不出這麼簡單的死活題？

　　為了那1%的小概率，我用得著額外出50萬，去買個“保險”嗎？

　　6、黑棋準備殺這塊白棋了。這位9段異常謹慎，他連續在別處“打將”以拖延時間，可見他的小心，哪怕這道死活題對他來說太簡單了。

　　然而，黑天鵝出現了，他居然走錯了！

　　觀戰區嘩然了，天吶，這個9段怎麼啦？

　　7、黑棋怎麼都不可能輸的棋，輸掉了。

　　於是，我的“煮熟的鴨子”飛了，“板上釘釘”的210萬收益沒了，自己白手起家賺來的240萬本金，也灰飛煙滅。

　　（以上皆為虛擬幣。）

　　那一刻的我，深深地意識到：

　　所謂的勝券在握，真的只是一個概率問題。

　　什麼事情都可能發生。

　　沒有尾部對沖的投資者，就不該留在賭桌上。

　　最後

　　總結十條：

　　1、這個世界的不確定性，在空間上是由很多個不確定性疊加在一起構成的，在時間上則可能反轉反轉再反轉。

　　2、別指望靠某一層的“精確預測”來消除不確定性，“無知”永遠包裹著“已知”。你需要在“無知”層構建安全氣囊，守護你的“已知”。

　　3、當你對某個事物有一個主觀判斷，試一下兩頭看：往回想一下這個事物的基礎概率，往後算一下這個事物的賠率、期望值和尾部風險。

　　4、像下棋一樣，當一件事情發生時，你要想：下一步呢？再下一步呢？記住在競技場上一盤棋唯一的目的是贏棋，而非局部的得失。

　　5、對於可能致命的事情，永遠不要心存僥倖心理。這時候你要相信“別去你媽媽（或老婆）不讓去的地方”這類常識，而不是專家們口中的“幾乎不可能發生”，也別輕信“超過90%的大概率事件”。除非你有足夠與其對沖的保險。

　　6、遠離對股市的短期預測，遠離那些自稱料事如神的“大師”。人對控制經濟的幻覺，和對征服大自然的幻覺，是類似的。

　　7、歷史只在如何虧錢這件事上“很押韻”，要想賺錢總要應對“前所未見的新情況”。“保命”比“賺大錢”更重要。

　　8、個人買股票做投資，拿“閒錢”，千萬別加槓桿，不管你區分石頭和熊的準確度有多高，哪怕勝率極高。

　　例如段永平，連房子都不貸款，一方面是錢多，一方面是沒必要，萬一是熊呢？

　　9、從你不贊同的人那裡學習，在你犯錯的地方變強大，從你害怕發生的小概率事件中獲得收益。

　　10、做時間的朋友，是指：

　　你知道自己和時間有一個沉甸甸的約會，

　　但你一點兒都不擔憂，

　　這個約會什麼時候發生。